▷ METROLOGÍA Y ANÁLISIS DE SISTEMAS DE MEDICIÓN (MSA)

¿Qué es la Metrología?

La metrología es la ciencia de la medición y es importante en áreas como la ciencia, la manufactura y el comercio. La metrología nos permite conocer la precisión de las mediciones y garantizar que se utilicen estándares comunes. En ciencia, esto significa que sabemos si un experimento realmente prueba lo que parece probar o si el resultado podría deberse a una medición inexacta. En la fabricación significa que podemos hacer piezas que encajen y funcionen como fueron diseñadas. En el comercio significa que sabemos cuánto de algo estamos comprando realmente.

Incertidumbre de la medición

Lo primero que debe comprender acerca de la metrología es que ninguna medición es exacta o segura. Si le mostrara un perno y le preguntara cuánto mide, podría decir: «Mide al rededor de 100 mm». El uso de la expresión «al rededor de» implica que existe cierta incertidumbre en su estimación.

Todas las medidas tienen incertidumbre y cuanto más grandes son los límites que establecemos, más confianza tenemos

Todas las medidas tienen incertidumbre; de hecho, una medición es solo una estimación, podría ser una estimación mucho mejor que la que puede hacer con solo mirar algo, pero una medición nunca puede decirle el valor exacto. En metrología siempre debemos considerar esta incertidumbre al realizar una medición.

Confianza en las mediciones

Relacionado con la incertidumbre está el concepto de confianza. Pensando de nuevo en mirar un perno y estimar la longitud, podríamos decir “son unos 100 mm más o menos 5 mm”. Esto está asignando límites a nuestra incertidumbre. Estaríamos más seguros al decir que el perno es de 100 mm más o menos 10 mm de lo que estaríamos al decir que está dentro de los 5 mm. Cuanto mayor sea el rango de incertidumbre que asignamos, mayor será nuestra confianza en que abarca el valor «verdadero». Podría mirar el perno y decir que estoy 70% seguro de que es 100 mm más o menos 5 mm y 90% seguro de que está dentro de +/- 10 mm. La incertidumbre de mi estimación es de +/- 10 mm a un nivel de confianza del 90%.

En metrología debemos tener muy claro el nivel de nuestra incertidumbre en un nivel de confianza dado. Podemos realizar una evaluación de la incertidumbre que incluye análisis y experimentos para determinar la incertidumbre de una medición. La mayoría de las incertidumbres siguen la distribución normal. Para una distribución normal, tendríamos un 67% de confianza de que el valor real está dentro de 1 desviación estándar del valor medido, un 95% de confianza está dentro de 2 desviaciones estándar y un 99,7% de confianza está dentro de 3 desviaciones estándar. Las desviaciones estándar y la distribución normal se explican en detalle más adelante.

Normal Distribution Showing Confidence Intervals - an important concept in metrology

Muchas cantidades variables se distribuyen normalmente: con 68,2% de los valores dentro de 1 desviación estándar del promedio medio, 95,4% dentro de 2 desviaciones estándar y 99,7% dentro de 3 desviaciones estándar

Cuanto mayor sea el rango de incertidumbre que asignamos, mayor será nuestra confianza en que abarca el valor «verdadero».

Calibración y trazabilidad en metrología

Es muy importante que todos usemos los mismos estándares de medición en todo el mundo. Cuando se fabrican las piezas, se ajustan las máquinas y se comprueban las piezas acabadas mediante medidas. Al utilizar los mismos estándares de medición, sabemos que una tuerca fabricada en China se ajustará a un perno fabricado en los EE. UU. La calibración es la forma en que los estándares se transfieren de un país a otro y de un instrumento a otro. Los estándares de referencia primarios para las unidades de medida del SI se mantienen en Francia y cada país compara sus estándares nacionales con estos. Los laboratorios de calibración comparan sus estándares con los estándares nacionales y luego los utilizan para calibrar los instrumentos.

La calibración simplemente significa comparar una medida con otra. Por ejemplo, cuando se hace una regla, se puede comparar con una regla de referencia para determinar dónde se colocan las marcas. Esta es una calibración simple. Las marcas no estarán exactamente en las mismas posiciones que las de la regla de referencia; habrá cierta incertidumbre en el proceso de calibración. La regla de referencia en sí tampoco tendrá marcas exactamente en las posiciones correctas, ya que hubo cierta incertidumbre cuando se calibró. La regla tiene incertidumbre tanto del estándar de referencia utilizado para calibrarla como del proceso de calibración, por lo tanto, un instrumento siempre debe tener una incertidumbre mayor que el instrumento que se utilizó para calibrarlo. Cuando se calibra un instrumento, siempre se debe evaluar la incertidumbre de la calibración.

Traceability in metrology means that there is an Unbroken Chain of Calibrations back to the Primary Standard

Una medida rastreable es aquella que tiene una cadena ininterrumpida de calibraciones que regresa al patrón de referencia primario, con incertidumbres calculadas para cada calibración. La incertidumbre de la medición se hereda a lo largo de la cadena de calibraciones, de modo que la incertidumbre aumenta cuanto más nos alejamos del patrón de referencia principal. La trazabilidad desde la referencia primaria, a través de laboratorios de metrología acreditados y hasta los departamentos de metrología industrial, asegura que todos estemos trabajando con estándares comunes y conocemos la incertidumbre de las mediciones.

Análisis de sistemas de medición (MSA)

El análisis de sistemas de medición (MSA) es un enfoque alternativo que busca cuantificar la ‘precisión‘ de las mediciones, esto es equivalente a evaluar la incertidumbre de las mediciones, pero existen algunas diferencias clave que se explican en detalle más adelante.

Exactitud, precisión y veracidad

Dentro de MSA, la exactitud se define como la suma de veracidad y precisión. La veracidad, también conocida como «sesgo», es la diferencia entre la media de muchas mediciones y el valor de referencia. La precisión describe la precisión con la que las mediciones repetidas de la misma cantidad muestran los mismos resultados.

Metrología - Verdadero pero no preciso — Verdadero pero no preciso

Metrología - Preciso pero no verdadero — Preciso pero no verdadero (repetidamente incorrecto)

Repetibilidad y reproducibilidad del Medidor

La repetibilidad y la reproducibilidad son dos medidas de precisión. La repetibilidad mide cómo varían los resultados de una medición cuando la medición se repite en las mismas condiciones y en un período corto de tiempo. La reproducibilidad mide cómo varían los resultados de una medición cuando la medición se repite en condiciones cambiantes y durante largos períodos de tiempo. Los estudios de repetibilidad y reproducibilidad del sistema de medición (Gage R&R) son experimentos en los que diferentes cantidades son medidas múltiples veces por diferentes operadores para comprender la precisión de un proceso de medición. Esto se explica en detalle en las páginas siguientes.

Reglas de decisión para probar la conformidad

Si las mediciones son inciertas, ¿Cómo pueden probar algo? Por ejemplo, ¿una medición prueba que una pieza está fuera de tolerancia? Existen algunas reglas simples que nos permiten establecer, a un nivel de confianza estadístico dado, si una medición prueba o refuta la conformidad. También es posible que el resultado no sea concluyente, en cuyo caso es posible que deseemos realizar más mediciones con una incertidumbre reducida.

La tolerancia para una dimensión define un límite de especificación superior (USL) y un límite de especificación inferior (LSL). Por ejemplo, si una dimensión se especifica como 10 mm +/- 0,1 mm, entonces el USL es 10,1 mm y el LSL es 9,9 mm. Para demostrar la conformidad, a un nivel de confianza dado, debemos sumar la incertidumbre expandida (U), en ese nivel de confianza, al LSL y restar la incertidumbre expandida del USL.

The Conformance Zone must be reduced by the Uncertainty of Measurement - Decision Rules for Proving Conformance or Non-Conformance (at 95% confidence)

Reglas de decisión para probar la conformidad o no conformidad (al 95% de confianza)

En la siguiente sección explicaremos un poco más sobre la incertidumbre de la medición, introduciendo tipos de incertidumbre y los principios que deben entenderse para evaluar la incertidumbre.

Todas las mediciones tienen una incertidumbre que surge de muchas fuentes, como la repetibilidad, la calibración y el entorno. El cálculo de la incertidumbre total resultante de todas las fuentes implica primero estimar la contribución de cada fuente y luego determinar cómo se combinarán para dar una incertidumbre estándar combinada.

Fuentes de incertidumbre Tipo A y Tipo B

fuentes de incertidumbre se clasifican como Tipo A si se estiman mediante análisis estadístico de mediciones repetidas o Tipo B si se estiman utilizando cualquier otra información disponible. Por ejemplo, para encontrar la repetibilidad de un instrumento, simplemente podríamos medir la misma cantidad 20 veces y analizar los diferentes resultados que obtuvimos, esto sería una incertidumbre de Tipo A. Encontrar la incertidumbre en nuestro estándar de referencia de calibración mediante este método no sería práctico, para esto simplemente buscamos la incertidumbre en su certificado de calibración, esta es una incertidumbre de Tipo B.

Estadísticas básicas necesarias para la evaluación de la incertidumbre

Para dar valores de las incertidumbres, se requiere una comprensión de las estadísticas básicas; desviaciones estándar, distribuciones de probabilidad como la distribución normal y el teorema del límite central. Estos se explican a continuación.

Desviación estándar

Para encontrar la repetibilidad de un instrumento, podemos medir la misma cantidad 20 veces. Entonces tendremos 20 resultados de medición ligeramente diferentes que dan una idea de cuánto varía el instrumento al medir lo mismo, necesitamos encontrar un número que represente esta variación. El número más simple de encontrar sería el rango de los datos; el valor más grande menos el valor más pequeño, pero esto realmente no representaría muy bien la distribución de todas las mediciones y cuantas más mediciones hiciéramos, más grande sería, lo que sugiere que no es un método confiable. La desviación estándar es un número que se puede calcular, que es esencialmente el promedio medio de la distancia entre cada medición individual y el promedio de todas las mediciones. Esto se entiende mejor con un ejemplo….

La medida estándar de incertidumbre es la desviación estándar, por lo que una ‘incertidumbre estándar‘ significa una desviación estándar en la medición.

Distribuciones de probabilidad y el teorema del límite central

Voy a explicar qué es una distribución de probabilidad pidiéndole que se imagine tirando unos dados. Primero tira un dado. Puedes sacar un 1, 2, 3, 4, 5 o 6, y tienes las mismas posibilidades de sacar cualquiera de ellos. Si tira los dados 100 veces y traza un gráfico de barras del puntaje contra la frecuencia (la cantidad de veces que obtuvo ese puntaje), terminará con 6 barras, todas de igual altura. Estas barras forman una forma rectangular y esto se conoce como distribución rectangular; el resultado puede ser cualquier valor entre algunos límites. La incertidumbre debida al redondeo al incremento más cercano en la escala de un instrumento tiene una distribución rectangular.

Ahora considere lanzar 2 dados; A y B. puedes puntuar entre 2 y 12. Pero ahora no hay las mismas posibilidades de conseguir una puntuación. Solo hay una forma de puntuar 2 (A = 1 y B = 1), hay dos formas de puntuar 3 (A = 1 y B = 2, A = 2 y B = 1) y así sucesivamente. Las posibilidades siguen aumentando hasta llegar a un puntaje de 7, que puede surgir de seis permutaciones diferentes de dados, y luego las probabilidades disminuyen hasta llegar a un puntaje de 12 para el cual nuevamente solo hay una forma de tirarlo; ambos dados deben ser seises. Si graficamos estos puntajes en un gráfico de barras, obtenemos una distribución triangular. Esto es interesante porque no solo se aplica a los dados, si combinamos los efectos de dos eventos aleatorios cualesquiera con distribuciones rectangulares o magnitud similar, obtenemos una distribución triangular.

Si agregamos más dados, las cosas se vuelven aún más interesantes. El pico del triángulo comienza a aplanarse y los extremos comienzan a desprenderse para formar una forma de campana conocida como distribución normal. De hecho, el teorema del límite central establece que varias distribuciones independientes de cualquier forma se combinarán para dar una distribución normal. Por lo tanto, se puede suponer que la incertidumbre combinada se distribuye normalmente incluso cuando muchos de los componentes de la incertidumbre no lo están. Esto es útil, ya que si sabemos que nuestra incertidumbre está distribuida normalmente, entonces sabemos cuál es la probabilidad de que una medición tenga un error en más de una incertidumbre estándar (68%), en más de dos incertidumbres estándar (95%), etc.

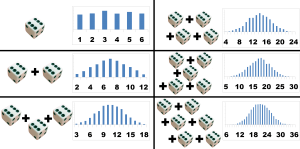
The Central Limit Theorem – One Die Gives and Equal Chance of a Number Between 1 and 6 but the Sum of 2 Dice is a Triangular Distribution between 2 and 12. More Dice tend towards a Normal Distribution

El Teorema del límite Central: un dado da igual probabilidad de un número entre 1 y 6, pero la suma de 2 dados es una distribución triangular entre 2 y 12. Más dados tienden a una distribución normal

Algunas fuentes típicas de incertidumbre

La incertidumbre de la medición puede surgir de muchas fuentes. Tiendo a centrarme en mediciones dimensionales, pero los principios de evaluación de la incertidumbre y muchas de las fuentes de incertidumbre se pueden aplicar a cualquier medición, por ejemplo, tiempo, temperatura, masa, etc. Algunas fuentes de incertidumbre que se encuentran en prácticamente todas las mediciones trazables son la incertidumbre del estándar de referencia utilizado para la calibración, la repetibilidad del proceso de calibración y la repetibilidad de la medición real. Las incertidumbres ambientales, como la temperatura, serán fuentes importantes de incertidumbre para muchas mediciones. La resolución o el redondeo pueden no ser una fuente significativa de incertidumbre para los instrumentos digitales que leen muchos lugares decimales más allá de la repetibilidad del sistema, pero a menudo es importante para instrumentos con una escala de lectura manual, como reglas, relojes comparadores, etc. fuente de incertidumbre para las mediciones dimensionales.

Errores de alineación

La alineación es una fuente común de incertidumbre en la medición dimensional. Por ejemplo, cuando se mide la distancia entre dos superficies paralelas, debe ser perpendicular a las superficies. Cualquier desviación angular de la trayectoria de medición perpendicular resultará en un error de coseno en el que la distancia real es la distancia medida multiplicada por el coseno de la desviación angular.

Cosine Error, Common Source of Uncertainty of Measurement

El error de coseno es una fuente común de incertidumbre de medición

Otro error de alineación común es el error de paralaje. Esto resulta de ver un marcador, que está separado por cierta distancia de la escala o del objeto que se está midiendo, en un ángulo incorrecto. Error de paralaje que se observa comúnmente cuando un pasajero en un automóvil lee el velocímetro. Otro ejemplo común es cuando las marcas en la superficie superior de una regla se utilizan para medir entre los bordes de una superficie. Si el ángulo de visión no es perpendicular a la regla, se producirá un error de paralaje.

Parallax error is commonly observed when a passenger in a car reads the speedometer or when using a ruler with the markings on the upper surface

El error de paralaje se observa comúnmente cuando un pasajero en un automóvil lee el velocímetro o cuando usa una regla con las marcas en la superficie superior.

El error de Abbe es similar al error de paralaje, pero en lugar de ser el resultado de la alineación de los ángulos de visión, es el resultado de la alineación de los ejes de la máquina. La distancia entre el eje a lo largo del cual se mide un objeto y el eje de la escala de medición del instrumento se conoce como Abbe Offset. Si la distancia a lo largo del objeto no se transfiere a la distancia a lo largo de la escala en una dirección perpendicular a la escala, se producirá un error. El tamaño de este error será la tangente del error angular multiplicado por el Desplazamiento de Abbe. Los instrumentos como los calibradores Vernier son susceptibles al error de Abbe ya que la escala de medición no es coaxial con el objeto que se mide. Los micrómetros no son susceptibles al error de Abbe.

Calipers are susceptible to Abbe Error since the Measurement Scale is not Co-Axial with the Axis of Measurement

Un instrumento es susceptible al error de Abbe si la escala de medición no es coaxial con el eje de medición

Repetibilidad y reproducibilidad

La repetibilidad se estima realizando una serie de mediciones, generalmente por la misma persona y en las mismas condiciones, y luego encontrando el estándar desviación de estas medidas. La reproducibilidad se estima realizando una serie de medidas, cada una por una persona diferente.

Un desafío en la evaluación de la incertidumbre de la medición es determinar qué fuentes de incertidumbre contribuyen a la repetibilidad observada. Por ejemplo, puede ser que los errores de alineación varíen aleatoriamente, lo que contribuye a la repetibilidad y, por lo tanto, no es necesario evaluarlos como un componente separado de la incertidumbre. La experiencia y el juicio a menudo juegan un papel en tales evaluaciones.

Un método para establecer tanto la repetibilidad como la reproducibilidad en una sola prueba es un ‘Análisis de varianza (ANOVA) de repetibilidad y reproducibilidad del sistema de medición (Gage R&R)’. Con este método, varias personas diferentes miden varias partes diferentes, pero cada parte generalmente solo mide 2 o 3 veces por cada persona. El orden de las partes es aleatorio. El análisis estadístico ANOVA se utiliza luego para separar la variación en los resultados que se debe a tres fuentes; la variación real del componente; la repetibilidad del sistema de medición; y la reproducibilidad de resultados entre diferentes personas. El R&R del sistema de medición es una muy buena manera de establecer los componentes de repetibilidad y reproducibilidad de la incertidumbre de la medición, pero el esfuerzo invertido en esto no debe considerarse un sustituto de la evaluación de otras fuentes de incertidumbre, como la calibración y el entorno.

Resolución

La incertidumbre de la medición debido a la resolución es el resultado de errores de redondeo. Para muchos instrumentos digitales, la resolución de lectura es muchas veces menor que la incertidumbre real del instrumento. En tales casos, los errores de redondeo debidos a la resolución del instrumento son insignificantes.

Para instrumentos más tradicionales, la resolución es a menudo una fuente importante de incertidumbre. El error máximo posible debido al redondeo es la mitad de la resolución. Por ejemplo, al medir con una regla que tiene una resolución de 1 mm, el error de redondeo será de +/- 0,5 mm que tiene una distribución rectangular. La conversión de una tolerancia con una distribución rectangular en una incertidumbre estándar se trata más adelante.

Rounding Errors Can be up to Half of the Resolution of an Instrument

Los errores de redondeo pueden ser hasta la mitad de la resolución de un instrumento

Temperatura

Las variaciones de temperatura afectan las mediciones de varias formas:

Expansión térmica del objeto que se mide y del instrumento utilizado para medirlo
Para mediciones interferométricas cambios en el índice de refracción
Para las mediciones ópticas que dependen de la luz siguiendo una trayectoria recta gradientes de temperatura causarán refracción que provocará la flexión de la luz y, por lo tanto, distorsiones

Calibración

Cualquier error en el estándar de referencia utilizado para calibrar un instrumento de medición se transfiere durante la calibración. Por lo tanto, los instrumentos heredan la incertidumbre de su estándar de calibración. El proceso real de calibración tampoco es perfectamente repetible; por lo tanto, se introduce una incertidumbre adicional a través del proceso de calibración.

Si la calibración ha sido realizada por un laboratorio de calibración acreditado, se dará una incertidumbre en el certificado de calibración. Ésta no es la incertidumbre de las mediciones realizadas con el instrumento; es simplemente el componente de incertidumbre debido a la calibración. Este punto a menudo se pasa por alto.

Al realizar una calibración, se debe realizar una evaluación completa de la incertidumbre para el proceso de calibración. La incertidumbre combinada para la calibración se convierte entonces en un componente de la incertidumbre para las mediciones tomadas con el instrumento.

Combinación de fuentes individuales de incertidumbre de medición

Una vez que se han identificado y cuantificado las fuentes individuales de incertidumbre de una medición, se debe calcular una incertidumbre combinada. Ésta es la incertidumbre real de medición para el proceso que se está considerando.

Como introducción al proceso de combinación de incertidumbre, asumiremos primero que todas las fuentes están distribuidas normalmente. Teniendo en cuenta la medida de un perno, supongamos que solo hay dos fuentes de incertidumbre, la expansión térmica del perno y la incertidumbre de la propia medida del calibrador. Por lo tanto, el resultado de la medición (y) vendrá dado por

y = X + ΔxT+ ΔxC

donde x es la longitud real, ΔxT es el error debido a la expansión térmica y ΔxC es el error debido a la propia medición del calibre.

A Simple Example of Combining Uncertainty for the Measurement of a Bolt using Callipers

Un ejemplo simple de combinación de incertidumbre para la medición de un perno con calibradores

El error debido a cada fuente se desconoce; cada fuente de error tiene una incertidumbre que define el rango de valores que podríamos esperar que tome. La probabilidad de que ambos errores sean máximos o mínimos al mismo tiempo es muy pequeña. Por lo tanto, simplemente sumar las incertidumbres sería demasiado pesimista. En cambio, las incertidumbres de los componentes se combinan estadísticamente para dar una incertidumbre combinada.

El resultado de la medición viene dado por y = f (x) donde x1, x2, etc. son entradas como la longitud real y los diversos errores. Cada entrada tiene una incertidumbre asociada u (xi). La incertidumbre combinada viene dada por: –

U_{c} ^{} \left(y\right)=\sqrt{\sum _{i=1}^{N}\left[\frac{\partial f}{\partial x_{i} } \right]^{2} u^{2} \left(x_{i} \right) }

Para casos simples, como nuestro ejemplo de los calibradores que miden el perno, donde

y = x1 + x22… xn

Las derivadas parciales serán todas iguales a uno, de modo que

\begin{array}{l} {\frac{\partial f}{\partial x_{i} } =1\quad \Rightarrow } \\ {U_{c} ^{} \left(y\right)=\sqrt{\sum _{i=1}^{N}\left[\frac{\partial f}{\partial x_{i} } \right]^{2} u^{2} \left(x_{i} \right) } =\sqrt{\sum _{i=1}^{N}u^{2} \left(x_{i} \right) } } \end{array}

Aplicando esto a el ejemplo

y = X + ΔxT+ ΔxC

La longitud real (X) no tiene incertidumbre, dejando dos fuentes de incertidumbre; la incertidumbre en el error debido a la expansión térmica u (ΔxT); y la incertidumbre en el error debido a la propia medición del calibre u (ΔxC). Por lo tanto, la incertidumbre combinada es simplemente

U_{c} ^{} \left(y\right)=\sqrt{u^{2} \left(\Delta x_{T} \right)+u^{2} \left(\Delta x_{C} \right)}

Esta información se puede utilizar para crear un presupuesto de incertidumbre simple. Primero se estima la incertidumbre estándar para cada fuente de incertidumbre.

A table listing the standard uncertainty for each source of uncertainty of measurement

En este presupuesto de incertidumbre simple para una medición de calibre, primero se estima cada fuente de incertidumbre.

Existe una relación funcional simple en la que los errores simplemente se agregan al valor real para obtener el resultado de la medición. Por lo tanto, la incertidumbre combinada es simplemente la raíz cuadrada de la suma de la incertidumbre al cuadrado de cada componente (RSS). La incertidumbre combinada se multiplica por un factor de cobertura para dar la incertidumbre al nivel de confianza requerido (la incertidumbre expandida).

The simple uncertainty budget is completed by calculating the combined standard uncertainty and expanded uncertainty

El presupuesto de incertidumbre simple se completa calculando la incertidumbre estándar combinada y la incertidumbre expandida.